4. Modern Cryptography

1. 4.1. Interlude: Primes
2. 4.2. Interlude: Euler’s Phi Function
3. 4.3. Interlude: Binary Exponentiation
4. 4.4. Interlude: Primality Testing
5. 4.5. RSA
6. 4.6. Interlude: Order
7. 4.7. Elgamal
8. 4.8. Diffie-Hellman
9. 4.9. Interlude: Elliptic Curves Over the Reals
10. 4.10. Interlude: Elliptic Curves Mod a Prime
11. 4.11. Elliptic Curve Diffie-Hellman
12. 4.12. Interlude: Quadratic Residues
13. 4.13. Elliptic Curve Elgamal

4.1. Interlude: Primes

Here is a definition that you may have seen before:

For example, 5 is prime since 1 and 5 are its only divisors. 4, on the other hand, is not prime, since 2 is a divisor of 4 (in addition to 1 and 4).

Ubiquity of Primes

There is a very important sense in which primes are “ubiquitous” — namely, that every positive integer \(n \geq 2\) can be written (uniquely!) as a product of primes. For example, \(18 = 2 \cdot 3^2\), and both 2 and 3 are prime. An expression of an integer \(n \geq 2\) as a product of primes is called a prime factorization of \(n\).

For example, \(60 = 2^2 \cdot 3^1 \cdot 5^1\) is a prime factorization of 60. It is the only one: we could instead write \(60 = 5^1 \cdot 2^2 \cdot 3^1\), but besides this kind of reordering of the factors, there is nothing else.

The fundamental theorem of arithmetic is likely deeply ingrained in your mathematical intuition, but it is in fact a “theorem” — it is something that can and should be proved. The proof makes use of some of the machinery we’ve already seen, so let’s prove it!

Proof of the fundamental theorem of arithmetic. The existence statement is a great example of a proof by “strong induction.” We start by noticing that 2 is prime, so it is its own prime factorization. Now suppose that \(n \geq 2\) and that every integer \(m\) such that \(2 \leq m < n\) has a prime factorization. If \(n\) itself is prime, it is again its own prime factorization and we are done. If \(n\) is composite, by definition it has a divisor \(m\) such that \(2 \leq a < n\). This means that \(n/a = b\) is an integer with \(2 \leq b < n\) as well. By assumption, both \(a\) and \(b\) have prime factorizations; since \(n = ab\), multiplying those prime factorizations together gives us a prime factorization of \(n\).

For the uniqueness statement, suppose for a contradiction that there is an integer greater than or equal to 2 that can be written as a product of primes in two different ways. But then there must be a smallest such integer; let’s call that integer \(n\). By assumption, we have \(n = p_1 \cdots p_t = q_1 \cdots q_u\). Since \(p_1\) divides the left-hand side, it must also divide the right hand side. We must have \(\gcd(p_1, q_i) = 1\) or \(p_1\), but it cannot be equal to 1 for all \(i\) by Euclid’s lemma. Thus there exists some \(i\) such that \(\gcd(p_1, q_i) = p_1\), which means that \(p_1\) divides \(q_i\). Since \(q_i\) is also prime, we must have \(p_1 = q_i\), so then we can cancel \(p_1 = q_i\) from both sides to see that \(p_2 \cdots p_t = q_1 \cdots q_{i-1} q_{i+1} \cdots q_u\). But now we have two distinct prime factorizations of a number that’s strictly smaller than \(n\), which is a contradiction! \(\Box\)

Scarcity of Primes

Having made the observation that primes are “ubiquitous,” we now turn to two important senses in which primes are “scarce.” The first sense is a literal sense: as a proportion of all integers, very few integers end up being prime!

Let me also just mention in passing that the scarcity of primes we see in the plot above is formalized by the statement of “Prime number theorem,” which is a difficult but landmark theorem in analytic number theory.

Difficulty of Factoring

The second sense in which primes are “scarce” is that prime factorizations are extremely difficult to actually calculate, even for moderately large numbers.

The naive way to find a prime factorization is to just start going through to see what’s a factor. Let’s say, for example, that we want to factor 75. We check first that 2 does not divide 75. We then see that 3 does divide 75, and we’re left with 25. Now 3 no longer divides 25. 4 also does not divide 25 (which we anyway knew since we already saw that 2 didn’t divide 75), but 5 does divide 25, so we divide again and we’re left with 5. And 5 divides itself again, which leaves a 1 in the end and we can stop. This procedure tells us that \[ 75 = 3^1 \cdot 5^2. \] As you might imagine, this procedure gets extremely slow as the number gets larger — or more specifically, as the prime factors of the number get larger.

Computational number theorists have worked out lots of deep, sophisticated, and clever techniques (which we do not have time to discuss this quarter) to speed this process up, but no one has yet found a factorization algorithm for classical computers that is substantially better than the naive method we just described. If you’ve seen some computational complexity theory, you might know what it means to say that there is no known factorization algorithm which is polynomial in the number of digits in the input.

98451812256345345465436565462354534524552443341112317013333179953

We’ll see below that the difficulty of factoring can be leveraged to build modern cryptosystems that are in widespread use today.

Incidentally, you may have noticed two things in the discussion above. First, we said only that no substantially better algorithm is known, not that there is no such algorithm. We do not have a proof that prime factorization cannot be done “quickly” (ie, in polynomial time), and it is an open problem in mathematics and/or theoretical computer science to prove this. (Or to disprove it, but given how much time and money people have put into trying to find a quick factorization algorithm, this seems unlikely…!)

The second thing you may have noticed is the phrase “classical computers.” In fact, we do know efficient factorization algorithms for quantum computers! Quantum computing hardware has not yet caught up to our theoretical knowledge, so our modern cryptosystems are still safe for now, but this state of affairs won’t last for much longer. We will soon need new cryptosystems that are secure against quantum computers.

The difficulty of factoring suggests that the function \(\mu\), which takes as input two prime numbers \(p\) and \(q\) and outputs the product \[ \mu(p, q) = pq \] is our first example of a one-way function. It’s very easy to compute the product of two primes; but, if the primes are large, it’ll be very hard to invert this function (ie, to find the prime factors of some given number that has two large prime factors). This is the one-way function on which RSA is based, as we will see soon. But first, we need to develop still more theory.

4.2. Interlude: Euler’s Phi Function

Here’s an idea that we’ve already seen before:

For example, when we were counting that there are 312 affine encryption functions available in English, part of the process involved counting the number of numbers relatively prime to 26, and we found that it was 12. We can now say this more succinctly by saying \(\phi(26) = 12\).

In fact, there is a nice formula for \(\phi(n)\) in terms of the prime factorization of \(n\), which we now describe. First, let us record the following property.

Proof sketch. Observe that \(\gcd(r, ab) = 1\) if and only if \(\gcd(r, a) = 1\) and \(\gcd(r, b) = 1\). Let’s arrange the numbers 0 through \(ab-1\) in a grid as follows. \[ \begin{matrix} 0 & 1 & 2 & \cdots & b-1 \\ b & b+1 & b+2 & \cdots & 2b-1 \\ 2b & 2b+1 & 2b+2 & \cdots & 3b-1 \\ (a-1)b & (a-1)b + 1 & (a-1)b + 2 & \cdots & ab-1 \end{matrix} \] All of the numbers in a given column are congruent mod \(b\), so if if one of these numbers is relatively prime with \(b\), then every number in that column must also be relatively prime with \(b\). Thus there are \(\phi(b)\) columns that are relatively prime with \(b\), and it is sufficient to show that each of those columns has \(\phi(a)\) entries which are relatively prime with \(a\).

The entries in the \(r\)th column are of the form \(sb + r\) for \(s\) varying between 0 and \(a-1\). Since \(\gcd(a, b) = 1\), every congruence class mod \(a\) is represented exactly once in each column. We know that \(\phi(a)\) of the congruence classes mod \(a\) are relatively prime to \(a\), so we are done. \(\Box\)

This brings us to the promised formula.

We can now calculate Euler’s phi function, but the reason this number is important is because of the following very important theorem.

Proof sketch. Let \(r_1, \dotsc, r_{\phi(n)}\) be the integers between 0 and \(n-1\) which are relatively prime to \(n\). Since \(\gcd(a, n) = 1\), the integers \(ar_1, \dotsc, ar_{\phi(n)}\) represent the same congruence classes, but maybe in a different order. Since multiplication of integers is commutative, we have \[ r_1 \cdots r_{\phi(n)} \equiv (ar_1) \cdots (ar_{\phi(n)}) = a^{\phi(n)} r_1 \cdots r_{\phi(n)} \pmod{n}. \] We can now multiply mod \(n\) by \(r_{\phi(n)}^{-1}\), and \(r_{\phi(n)-1}^{-1}\), and so forth, all the way down to \(r_1^{-1}\) to conclude that \[ 1 \equiv a^{\phi(n)} \pmod{n}, \] which is what we wanted to show. \(\Box\)

Let’s consider an example. Notice that \(20 = 2^2 \cdot 5\), so \[ \phi(20) = 2^1(2-1) \cdot 5^0 (5-1) = 8. \] This means that \(a^{\phi(20)} = a^8 \equiv 1 \bmod{20}\) for any \(a\) that is relatively prime to 20. For example, consider \(a = 3\). We do in fact have \(\gcd(3, 20) = 1\), and we can check explicitly using the Modular Arithmetic Theorem that: \[ \begin{aligned} 3^2 &= 9 \\ 3^4 &= (3^2)^2 \equiv 9^2 = 81 \equiv 1 \pmod{20} \\ 3^8 &= (3^4)^2 \equiv 1^2 = 1 \pmod{20}. \end{aligned} \] We can also use this Euler’s theorem to compute very very large powers of some number. Suppose, for example, that we want to compute \(7^{20232023} \bmod{20}\). Notice that \(20232000\) is divisible by 8, so we have \[ 20232023 = 20232000 + 23 \equiv 23 \equiv 7 \bmod{8}. \] In other words, this means that \(20232023 = 8q + 7\) for some integer \(q \geq 0\). We then have \[ 7^{20232023} = 7^{8q + 7} = (7^8)^q 7^7 \equiv 1^q 7^7 = 7^7 \pmod{20}. \] So now we just have to compute \(7^7 \bmod{20}\), which we can do as follows: \[ \begin{aligned} 7^2 &= 49 \equiv 9 \bmod{20} \\ 7^4 &= (7^2)^2 \equiv 9^2 = 81 \equiv 1 \bmod{20} \\ 7^7 &= 7^4 \cdot 7^2 \cdot 7 \equiv 1 \cdot 9 \cdot 7 = 63 \equiv 3 \bmod{20} \end{aligned} \] We thus have \(7^{20232023} \bmod{20} = 3\).

Notice that we were able to do this remainder calculation without having to actually compute \(7^{20232023}\). This is an important observation, because we’ll see below that RSA will require us to do similar remainder calculations even when the numbers are so large that it is completely infeasible for computers to actually calculate out the result of the exponentiation. We’ll discuss this point in more detail in the following section.

Meanwhile, here are some exercises to practice with Euler’s theorem!

4.3. Interlude: Binary Exponentiation

With Euler’s theorem in hand, we can now compute large powers in modular arithmetic very quickly. We saw this briefly above, but let’s now explain the process systematically. Suppose we have a positive integer \(n\) and an integer \(a\) with \(\gcd(a, n) = 1\), and that we want to compute \(a^m \bmod{n}\) for some large number \(m\).

The first step is to calculate \(r = m \bmod{\phi(n)}\). Indeed, if we do this, then we have \(m = \phi(n)q + r\), so \[ a^m = a^{\phi(n)q + r} = (a^{\phi(n)})^q a^r \equiv 1^q a^r = a^r \pmod{n} \] using Euler’s Theorem (and the Modular Arithmetic Theorem). This immediately reduces the power we have to compute substantially.

We can then compute \(a^r \bmod{n}\) using a technique called “binary exponentiation.” The idea is fairly straightforward in examples, though it can becomes hard to understand in the abstract, so let’s start by considering an example.

Suppose we find that \(r = 25\). How can we compute \(a^r \bmod{n}\)? One naive thing we could do is multiply \(a\) by itself mod \(n\) repeatedly; this would require 25 multiplications mod \(n\). Here’s another idea. Let’s start squaring repeatedly:

• Find \(a^2 \bmod{n}\).
• Find \(a^4 = (a^2)^2 \bmod{n}\) by squaring the result of the previous step.
• Find \(a^8 = (a^4)^2 \bmod{n}\) by squaring the result of the previous step.
• Find \(a^{16} = (a^8)^2 \bmod{n}\) by squaring the result of the previous step.

If we square again, we’ll go past \(r = 25\), so we’ll stop there. We now want to figure out how to find \(a^{25}\) using the powers of \(a\) we’ve already computed. Notice that \(25 = 16 + 8 + 1\), so \[ a^{25} = a^{16+8+1} = a^{16} a^8 a^1, \] and we already know \(a^{16}, a^8\), and \(a\) mod \(n\), so we can compute \(a^{25} \bmod{n}\) by multiplying these three values together mod \(n\). Notice that this required only 6 multiplications total — much less than the 25 of the naive method!

Let’s see this entire process in action before describing the binary exponentiation part in the abstract. Suppose we want to compute \[ 3^{4398391} \bmod{80}. \] We first compute \(\phi(80) = 32\), and that \(4398391 \equiv 23 \bmod{32}\). Thus \(3^{4398391} \equiv 3^{23} \bmod{80}\) by Euler’s Theorem. We now use binary exponentiation: \[ \begin{aligned} 3^2 &= 9 \\ 3^4 &= (3^2)^2 = 9^2 = 81 \equiv 1 \bmod{80} \\ 3^8 &= (3^4)^2 \equiv 1^2 = 1 \bmod{80} \\ 3^{16} &= (3^8)^2 \equiv 1^2 = 1 \bmod{80} \\ 3^{23} &= 3^{16 + 4 + 2 + 1} = 3^{16} 3^4 3^2 3 \equiv 1 \cdot 1 \cdot 9 \cdot 3 = 27 \bmod{80} \end{aligned} \]

The “repeated squaring and then multiplying together” part of this process is very closely related to finding binary representations of integers. Here is the definition:

For example, the binary representation of 25 is 11001 because \[ 1 + 0 \cdot 2 + 0 \cdot 2^2 + 1 \cdot 2^3 + 1 \cdot 2^4 = 1 + 8 + 16 = 25. \] It is not clear at all from the definition how to find this binary representation, but here is the algorithm for doing this!

For example, suppose we want to calculate the binary representation of 193. We divide 193 by 2, and then repeatedly divide the quotient by 2: \[ \begin{aligned} 193 &= 96 \cdot 2 + 1 \\ 96 &= 48 \cdot 2 + 0 \\ 48 &= 24 \cdot 2 + 0 \\ 24 &= 12 \cdot 2 + 0 \\ 12 &= 6 \cdot 2 + 0 \\ 6 &= 3 \cdot 2 + 0 \\ 3 &= 1 \cdot 2 + 1 \\ 1 &= 0 \cdot 2 + 1 \end{aligned} \] We’ve now hit a quotient of 0, so we stop dividing. The binary representation is the sequence of remainders we found, with the leftmost bit being the last remainder we found and the rightmost bit being the first remainder we found. In other words, the binary representation of 193 is 11000001.

There’s a technical remark worth making here for those who are interested in computation. The above process is an “algorithm,” but it’s an algorithm that only human beings really have to perform…! A computer doesn’t have to go through the above process to find the binary representation, because a computer will already know the binary representation of any integer: binary representations are how computers talk about integers!

We can now state the general fact about binary exponentiation we described in the context of examples above:

4.4. Interlude: Primality Testing

We have one more theoretical ingredient to discuss for now: how can we quickly figure out if a number is prime? Remember that factoring is computationally expensive, so it’s not a good idea to try to figure out that a number is prime by factoring it!

It turns out that there are a number of fast strategies for testing primality. Here we’ll discuss one called the Miller-Rabin test. To explain how the this test works, we need to establish some theoretical preliminary results.

Proof. Observe that \(x^2 \equiv 1 \pmod{n}\) implies \[0 \equiv x^2 - 1 = (x-1)(x+1) \pmod{n}, \] which means that \(n\) divides \((x-1)(x+1)\). Since \(n\) is prime, Euclid’s lemma implies that \(n\) divides either \(x-1\) or \(x+1\), which means we have either \(x-1 \equiv 0 \pmod{n}\) or \(x+1 \equiv 0 \pmod{n}\). In other words, we have either \(x \equiv 1 \pmod{n}\) or \(x \equiv -1 \pmod{n}\), respectively. \(\Box\)

Proof. Since \(1 \leq a \leq n-1\) and \(n\) is prime, we have \(\gcd(a, n) = 1\). Thus, by Euler’s Theorem, we know that \(a^{n-1} = a^{2^s d} \equiv 1 \pmod{n}\). This means that \(x_1 = a^{2^{s-1}d}\) is satisfies \[ x^2_1 = (a^{2^{s-1}d})^2 = a^{2^s d} \equiv 1 \pmod{n}, \] so by the previous lemma, we must have either \(x_1 \equiv -1 \pmod{n}\), in which case we’re done, or else \(x_1 \equiv 1 \pmod{n}\). In the latter case, we can repeat the same argument with \(x_1\) replaced by \(x_2 = a^{2^{s-2}d}\), and so on, all the way down to \(x_s = a^d\). \(\Box\)

Let’s see what this lemma is saying in an example. Consider \(n = 41\), which is prime. We then have \(n-1 = 40 = 2^3 \cdot 5\). In other words, we can take \(s = 3\) and \(d = 5\) in the above lemma. Suppose we fix some integer \(a = 17\). Since \(s = 3\), we have 4 congruences in our list, and one of them should then be true, so let’s check which one! We first compute \(17^5 \equiv 27 \pmod{41}\) using binary exponentiation (as described in the previous section). This is not \(\pm 1\), so the first two congruence in the list fail. We then have \[ 17^{2 \cdot 5} = (17^5)^2 \equiv 27^2 \equiv 32 \bmod{41} \] so the third congruence also fails. But then we have \[ 17^{2^2 \cdot 5} = (17^{2 \cdot 5})^2 \equiv 32^2 \equiv 40 \equiv -1 \pmod{41} \] so the last congruence is in fact true!

The Miller-Rabin Lemma leads us to the following definition:

Using this definition, the Miller-Rabin Lemma can be restated as saying simply that “every prime number is a strong probable prime to any base.” This is equivalent to the contrapositive, ie, the statement that “if \(n\) is not a strong probable prime to some base \(a\), then \(n\) must be composite.”

Consider, for example, \(n = 25\). Of course, this number is small enough that we can see right away that it is not actually prime! But let’s see what’s going on with this notion of strong probable primes. Observe that \(n-1 = 24 = 2^3 \cdot 3\), so we have \(s = 3\) and \(d = 3\). Suppose first that we choose a base of \(a = 7\). Then \[ \begin{aligned} 7^3 &\equiv 18 \pmod{25} \\ 7^{2 \cdot 3} &= (7^3)^2 \equiv 18^2 \equiv 24 \equiv -1 \pmod{25} \end{aligned} \] so this says that 25 is a strong probable prime to base 7. If we instead choose \(a = 2\), then we have \[ \begin{aligned} 2^3 &= 8 \\ 2^{2 \cdot 3} &= (2^3)^2 = 8^2 \equiv 64 \equiv 14 \pmod{25} \\ 2^{2^2 \cdot 3} &= (2^{2 \cdot 3})^2 \equiv 14^2 \equiv 21 \pmod{25} \end{aligned} \] Thus \(n\) is not a strong probable prime to base 2, and 2 is a witness to the compositeness of 25.

The idea now is as follows. If \(n\) is composite, the most of the possible choices of base \(2 \leq a \leq n-2\) will in fact be witnesses for the compositeness of \(n\). This means that, if we try several such bases and none of them turn out to be a witness for compositness, we can be quite sure that \(n\) is in fact prime!

We’ve just described the Miller-Rabin primality test:

If we do \(k\) repetitions, the probability of a false positive is less than \(4^{-k}\). This gets small very quickly! For example, if we do just 10 repetitions, the probability of a false positive is about one in a million!

If you don’t like the idea of a probabilistic algorithm, you may be interested in reading about the AKS Primality Test, which is a fully deterministic algorithm that runs in polynomial time (ie, polynomial in the number of digits in the input). Note, though, that the AKS primality test often runs much slower than the Miller-Rabin test…! If you like, you can also read about deterministic variants of the Miller-Rabin test.

The upshot is that we can quickly check if a number is prime without having to factor it. This also gives us an algorithm for generating large prime numbers: basically, just keep generating random numbers until we find one that’s prime!

4.5. RSA

RSA is a cryptosystem named after Ron Rivest, Adi Shamir, and Leonard Adleman, who publicly described the algorithm in 1977. The GCHQ mathematician Clifford Cocks developed an equivalent system back in 1973, but his work was not declassified until 1997.

Let’s start by discussing how RSA works. We’ll then talk about why it works, and finally about why it’s secure (or at least, probably secure for now).

How to Convert Text Messages to Numbers

We first need a preliminary discussion about how to convert text messages into integers, since RSA only allows us to transfer integers. A variety of methods could be employed to make this happen, but one simple idea is for her to encode a message in the usual way (remove all non-alphabet characters and capitalize everything), and regard the resulting string as a number in base 26.

Suppose, for example, that Alice’s message is HIBOB. Under the usual letter-to-number correspondence (A is 0, B is 1, etc), these numbers correspond to the numbers 7, 8, 1, 14, 1 (in that order). We can then construct the integer \[ 1 \cdot 26^0 + 14 \cdot 26^1 + 1 \cdot 26^2 + 8 \cdot 26^3 + 7 \cdot 26^4 = 3340481. \] This is an integer representation of the message HIBOB in the sense that there is a straightforward algorithm to recover the plaintext: we use the same algorithm that we used to write a number in binary, but now we divide repeatedly by 26 instead. \[ \begin{aligned} 3340481 &= 128480 \cdot 26 + 1 \\ 128480 &= 4941 \cdot 26 + 14 \\ 4941 &= 190 \cdot 26 + 1 \\ 190 &= 7 \cdot 26 + 8 \\ 7 &= 0 \cdot 26 + 7 \end{aligned} \] We then look at the sequence of remainders, starting from the bottom (ie, 7, 8, 1, 14, 1), and associate to each of these remainders the corresponding letters to get back to the plaintext: HIBOB.

How RSA Works

Bob starts off by picking two distinct large primes \(p\) and \(q\). He computes \(n = pq\) and \(\phi(n) = (p-1)(q-1)\). He picks a random integer \(d\) between 0 and \(\phi(n)\) such that \(\gcd(d, \phi(n)) = 1\). He then computes \(e \equiv d^{-1} \pmod{\phi(n)}\) (eg, using the extended Euclidean algorithm). He then publishes the pair \((n, e)\) for the world to see; this is his public encryption key. He keeps the remaining numbers private.

Suppose Alice has a secret integer \(m\) between 0 and \(n-1\) that she wants to send to Bob. She encrypts \(m\) by computing \(c = m^e \bmod{n}\), and this is the ciphertext that she sends to Bob.

When Bob receives \(c\), he computes \(c^d \bmod{n}\). As it turns out, this must be \(m\), so he has received Alice’s message!

Why RSA Works

Proof. Observe that \(de \equiv 1 \pmod{\phi(n)}\), so there exists an integer \(k\) such that \(de = 1 + k\phi(n)\) and we have \[ c^d \equiv (m^e)^d = m^{ed} = m^{1 + k\phi(n)} \pmod{n}. \] Since \(0 \leq m < n\), it is therefore sufficient for us to show that \(m^{1 + k\phi(n)} \equiv m \pmod{n}\).

There are two cases. The first case is when \(\gcd(m, n) = 1\). Then Euler’s theorem says that \(m^{\phi(n)} \equiv 1 \pmod{n}\), so \[ \begin{aligned} m^{1 + k\phi(n)} = m \cdot (m^{\phi(n)})^k \equiv m \cdot 1^k = m \pmod{n}, \end{aligned} \] which is what we wanted to show.

The second case is when \(\gcd(m, n) \neq 1\). Since \(n = pq\) and \(0 \leq m < n\), it must be that \(\gcd(m, n) = p\) or \(\gcd(m, n) = q\). Without loss of generality, suppose \(\gcd(m, n) = p\). This means that \(m = xp\) for some integer \(x\) and also that \(m\) is not divisible by \(q\). Euler’s theorem tells us that \(m^{q-1} \equiv 1 \pmod{q}\), so \[ m^{k\phi(n)} = m^{k(p-1)(q-1)} = (m^{q-1})^{k(p-1)} \equiv 1^{k(p-1)} = 1 \pmod{q} \] so there exists an integer \(h\) such that \(m^{k\phi(n)} = 1 + hq\). Then \[ m^{1 + k\phi(n)} = m(1 + hq) = m + hmq = m + hxpq = m + hxn \equiv m \pmod{n}, \] which again is what we wanted to show! \(\Box\)

Why RSA is Probably Secure (for now…)

If Eve is eavesdropping on Alice and Bob’s communication, she knows Bob’s public key \((n, e)\) and she sees Alice’s ciphertext \(c\). She knows that \(c\) is the \(e\)th power mod \(n\) of Alice’s original message \(m\), so the security of RSA relies on the presumed difficulty of the following problem:

Most likely, there is no fast way of doing this — except for the way that Bob uses, which requires some secret knowledge! Bob needs to know the decryption exponent \(d\), which is an inverse of \(e\) mod \(\phi(n)\), and knowing that would seem to require knowing \(\phi(n)\).¹ The following lemma shows that knowledge of \(\phi(n)\) is actually equivalent to a knowledge of a factorization of \(n\), which is believed to be hard to find quickly!

Proof. Observe that \[ \phi(n) = (p-1)(q-1) = pq - p - q + 1 = n - p - q + 1, \] which means that \[ n+1-\phi(n) = p + q, \] which means that \[ (x-p)(x-q) = x^2 - (p+q)x + pq = x^2 - (n+1-\phi(n))x + n. \] In other words, \(p\) and \(q\) are the two roots of the quadratic polynomial \(x^2 - (n+1-\phi(n))x + n\), so if Eve knows how to quickly find \(\phi(n)\), she can then just apply the quadratic formula to this polynomial to factor \(n\) and find \(p\) and \(q\). \(\Box\)

In other words, the lemma tells us that, since it is believed that there is no fast factoring algorithm for classical (ie, non-quantum) computers, this tells us that Eve probably does not have a quick way of finding the decryption exponent \(d\) in the same way that Bob does.

4.6. Interlude: Order

Here is a basic definition that we will need in order to describe our next cryptosystems.

For example, suppose \(n = 7\) and \(a = 2\). We then compute: \[ \begin{aligned} 2^2 &= 4 \pmod{7} \\ 2^3 &= 8 \equiv 1 \pmod{7} \end{aligned} \] Thus 3 is the smallest positive exponent such that raising 2 to that power gives us something congruent to 1 mod 7, which means that \(\mathrm{ord}_7(2) = 3\).

Order Lemmas

Note that \(\phi(7) = 6\), and \(\mathrm{ord}_7(2) = 3\) happens to be a divisor of 6. This is no coincidence!

Proof. Let \(k = \mathrm{ord}_n(a)\). By Euclid’s Division Lemma, we can write \(m = kq + r\) where \(0 \leq r < k\). Then \[ 1 \equiv a^m = a^{kq + r} = (a^k)^q a^r \equiv 1^q \cdot a^r = a^r \pmod{n}. \] If \(r\) was nonzero, it would be a positive exponent strictly smaller than \(k\) which gives a number congruent to 1 mod \(n\), which contradicts the definition of \(\mathrm{ord}(a)\). Thus it must be that \(r = 0\), ie, that \(k\) divides \(m\).

By Euler’s theorem, we know that \(a^{\phi(n)} \equiv 1 \pmod{n}\). By what we have just shown, we therefore know that \(\mathrm{ord}_n(a)\) divides \(\phi(n)\). \(\Box\)

The First Order Lemma makes it a bit easier to compute the order of an element. Suppose, for example, that we are interested in \(n = 7\) and \(a = 3\). The lemma guarantees that \(\mathrm{ord}_7(3)\) must be a divisor of \(\phi(7) = 6\), so it can only be 1, 2, 3, or 6. We check: \[ \begin{aligned} 3^1 &\not\equiv 1 \pmod{7} \\ 3^2 &= 9 \equiv 2 \not\equiv 1 \pmod{7} \\ 3^3 &= 27 \equiv 6 \not\equiv 1 \pmod{7} \end{aligned} \] Thus \(\mathrm{ord}_7(3)\) cannot be 1, 2, or 3, so we know that it must be 6.

Proof. First suppose that \(i \equiv j \pmod{k}\). Then there exists an integer \(q\) such that \(i = kq + j\), so \[ a^i = a^{kq + j} = (a^k)^q a^j \equiv 1^q a^j = a^j \pmod{n} \] since \(a^k \equiv 1 \pmod{n}\). Conversely, suppose \(a^i \equiv a^j \pmod{n}\) and assume without loss of generality that \(i \geq j\). By multiplying both sides by \(a^{-1}\) mod \(n\) a total of \(j\) times, we find that \(a^{i-j} \equiv 1 \pmod{n}\), so the First Lemma About Orders tells us that \(k\) divides \(i - j\). In other words, \(i \equiv j \pmod{k}\).

For the final assertion, note that \(0, 1, 2, \dotsc, k-1\) are all incongruent mod \(k\), so \(a^0, a^1, a^2, \dotsc, a^{k-1}\) must all be incongruent mod \(n\). \(\Box\)

Primitive Roots and Discrete Logarithms

The First Lemma About Orders tells us that \(\phi(n)\) is the largest possible order mod \(n\) that any integer could have, since the order must always be a divisor of \(\phi(n)\). The situation when this maximum is achived gets a special name:

For example, we saw above that \(\mathrm{ord}_7(3) = 6 = \phi(7)\), so 3 is a primitive root mod 7.

The Second Lemma About Orders tells us that \(3^0, 3^1, 3^2, 3^3, 3^4, 3^5\) are all incongruent mod 7, but there are only 6 nonzero congruence classes mod 7, so the fact that all of the nonzero congruence classes mod 7 must be represented among the integers \(3^0, 3^1, 3^2, 3^3, 3^4, 3^5\). Let’s check this explicitly: \[ \begin{aligned} 3^0 &\equiv 1 \pmod{7} \\ 3^1 &\equiv 3 \pmod{7} \\ 3^2 &\equiv 2 \pmod{7} \\ 3^3 &\equiv 6 \pmod{7} \\ 3^4 &\equiv 4 \pmod{7} \\ 3^5 &\equiv 5 \pmod{7} \end{aligned} \] All of the nonzero remainders mod 7 appear in this list. This generalizes:

Our calculations above show that the discrete log base 3 of 6 mod 7 is 3, because \(3^3 \equiv 6 \pmod{7}\).

Existence of Primitive Roots

We haven’t yet shown that primitive roots always exist, and in fact, it is not true that primitive roots always exist. Here is the statement:

Proving this theorem would require a somewhat lengthy tangent, so I will omit it.

4.7. Elgamal

The Elgamal cryptosystem is a public-key cryptosystem like RSA, named after the Egyptian cryptographer Taher Elgamal.

How Elgamal Works

The process begins by Bob choosing a public key. He picks a prime number \(p\) and a primitive root \(g\) of \(p\). He chooses a random integer \(x\) with \(0 \leq x < p-1\). This is his private key. He then computes \(h = g^x \bmod{p}\) and his public key is the triple \((p, g, h)\).

Suppose now that Alice wants to send Bob a message. She first encodes her message as an integer \(m\) between 0 and \(p-1\). For example, we can use the same “base 26” strategy that we employed for RSA above. She then chooses a random integer \(y\) between 0 and \(p-1\) called the “ephemeral key.” Alice will have to choose a different ephemeral key for every message she sends, but Bob does not have to know the value of this key beforehand! Alice computes \(s = h^y \bmod{p}\), \(c_1 = g^y \bmod{p}\), and \(c_2 = ms \pmod{p}\). Note that she can compute \(s\) and \(c_1\) quickly using binary exponentiation! The pair \((c_1, c_2)\) is the ciphertext that she sends to Bob.

To decrypt the ciphertext \((c_1, c_2)\), Bob first computes \(c_1^x \bmod{p}\). Bob can do this quickly using binary exponentiation. Observe that \[ c_1^x \equiv (g^y)^x = g^{xy} = (g^x)^y \equiv h^y \equiv s \bmod{p}. \] In other words, Bob has now found the same value of \(s\) that Alice had, even though he does not know the value of the ephemeral key \(y\). He then computes an inverse mod \(p\) of \(c_1^x\) using the extended euclidean algorithm (which is also very efficient). He then computes the product \[ c_2 (c_1^x)^{-1} \equiv c_2 s^{-1} \equiv (ms)s^{-1} \equiv m \cdot 1 = m, \pmod{p} \] and he has recovered Alice’s message \(m\).

For example, suppose Bob picks the prime \(p = 4115549\), and \(g = 2\) is his primitive root. He then picks a random integer \(x = 2634326\). He can then compute \(h = g^x \bmod{p}\) quickly using binary exponentiation (eg, using the power_mod function in Sage); he finds \(h = 1149114\), so the triple \((4115549, 2, 1149114)\) is his public key. He must keep \(x = 2634326\) secret.

Now suppose that Alice wants to send Bob the message Hi Bob. As we did earlier in the RSA section, she can convert this to the integer \(m = 3340481\). She chooses an ephemeral key, say \(y = 2775147\). She keeps this value of \(y\) secret. She computes \(s = h^y \bmod{p}\) using binary exponentiation and finds \(s = 962840\). This \(s\) too, she keeps secret. She also computes \(c_1 = g^y \bmod{p}\) using binary exponentiation and finds \(c_1 = 621674\), and finally she computes \(c_2 = ms \bmod{p}\) and finds \(c_2 = 1911501\). The pair \((c_1, c_2) = (621674, 1911501)\) is then the ciphertext that she sends Bob.

Bob receives the pair \((c_1, c_2) = (621674, 1911501)\). He computes \(c_1^x \bmod{p}\) using binary exponentiation and finds that it is \(962840\), which is the same value that Alice had found for \(s\). He computes an inverse mod \(p\) (eg, using the Sage function inverse_mod) and finds \(s^{-1} \equiv 2329074 \bmod{p = 4115549}\). He then computes \[ c_2 s^{-1} \bmod{p} = 3340481, \] and he finally converts this back to the text HIBOB.

Why Elgamal is Probably Secure (for now…)

There are at least two strategies that Eve might employ to recover the plaintext \(m\) from the ciphertext \((c_1, c_2)\). She might try to find Bob’s decryption key \(x\) so that she can follow Bob’s decryption strategy, but to do this, she needs to find the discrete log base \(g\) of \(h\) mod \(p\). Alternatively, she might try to find Alice’s ephemeral key \(y\) (because she can then compute \(h^y\), and then \((h^y)^{-1} \equiv s^{-1} \pmod{p}\), and then \(c_2(h^y)^{-1} \equiv (ms)s^{-1} \equiv m \pmod{p}\)), but then she needs to find the discrete log base \(g\) of \(c_1\) mod \(p\).

In other words, it would seem that in either case, Eve needs to find a discrete log base \(g\) mod \(p\). The security of the Elgamal cryptosystem thus relies on the presumed difficulty of the following problem:

As \(p\) gets large, this problem seems to get intractible for classical computers. The naive method to solving this problem would be to try all the possible values of \(k\) from 1 up to \(p-1\), but this is at least linear in \(p\), which means it is at least exponential in the number of digits of \(p\). There are slightly faster algorithms than this, and these faster methods are implemented by Sage for its discrete log functionality, but they are not faster by much (more precisely, there is no known algorithm that accomplishes this task that is polynomial in the number of digits of \(p\)).

4.8. Diffie-Hellman

The Diffie-Hellman key exchange is not quite a cryptosystem for exchanging messages; it is a protocol that allows Alice and Bob to share a secret, but neither has full control over the content of the shared secret. Nonetheless, the shared secret can then be used as the key for a symmetric key cipher like a one-time pad.

The procedure is named after Whitfield Diffie and Martin Hellman, who published the protocol in 1976. The GCHQ mathematician Malcolm Williamson had developed the same protocol back in 1974, but his work was only declassified in 1997.

The procedure is as follows. Alice and Bob publicly agree to fix a prime \(p\) and a primitive root \(g\) mod \(p\). Alice then chooses a secret integer \(0 \leq a < p-1\) and sends Bob \(x = g^a \bmod{p}\). She can compute this value quickly using binary exponentiation. Bob similarly chooses a secret integer \(0 \leq b < p-1\) and sends Alice \(y = g^b \bmod{p}\). Alice computes \(s = y^a \bmod{p}\), and Bob computes \(s = x^b \bmod{p}\). The two values of \(s\) that Alice and Bob compute are the same, because \[ y^a \equiv (g^b)^a = g^{ab} = (g^a)^b \equiv x^b \pmod{p}. \] Thus Alice and Bob now share a secret, \(s\). Notice that neither has full control over the shared secret, so this cannot be regarded as Alice or Bob sending a message to the other.

There are many other cryptographic protocols besides the Diffie-Hellman key exchange which involve the presumed difficulty of the discrete log problem and which are not strictly about exchanging messages. Here are some examples:

• Schnorr signature algorithm
• Elgamal signature scheme
• DSA
• Zero-knowledge proofs of discrete logarithms

4.9. Interlude: Elliptic Curves Over the Reals

We’ll start with a discussion of elliptic curves over the real numbers in order to develop some geometric intuition about elliptic curves.

Here is a theorem that is useful to keep in mind, but we omit a proof because it will not be important for us in cryptography:

Given a Weierstrass equation, we can make a plot of the points \((x, y)\) in the plane that satisfy that equation. Here is a SageCell that makes these plots for you; make sure to play with it before moving forward!

What you should have found by playing with the above SageCell is that the set of points satisfying a nonsingular Weierstrass equation always roughly has one of the following shapes:

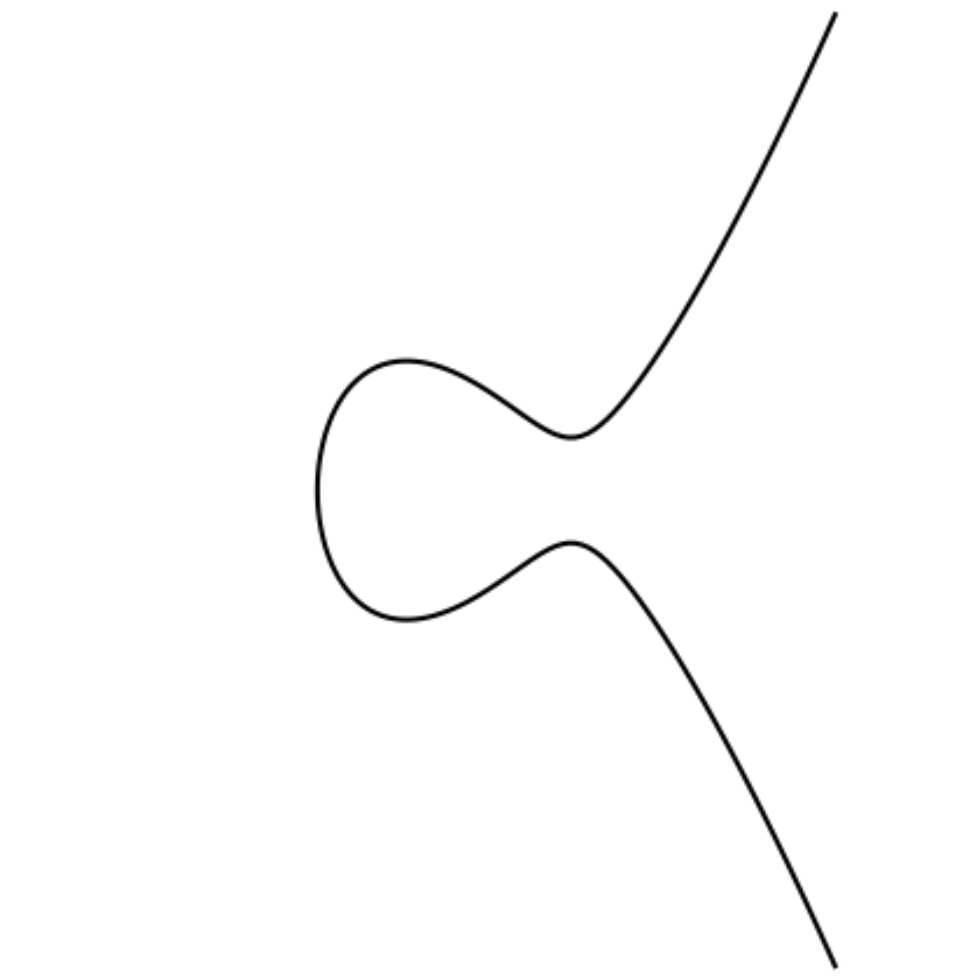
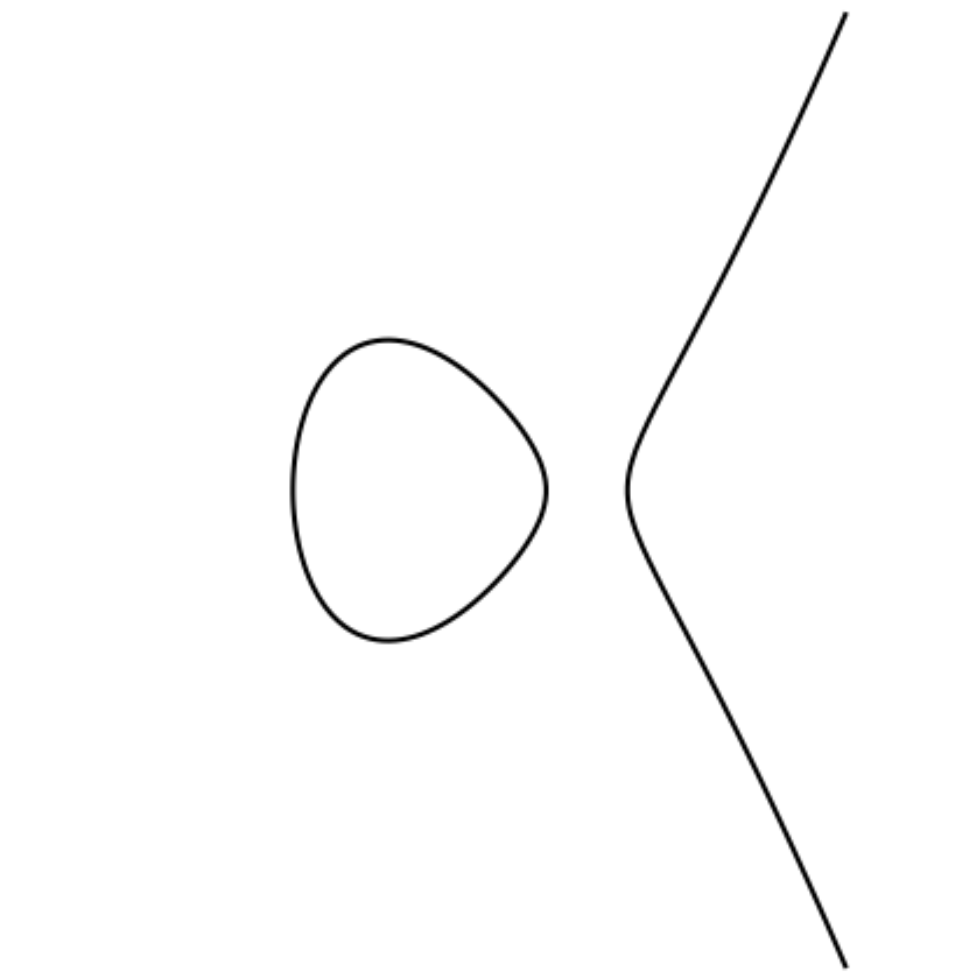
These curves have a lot of important geometry. To get started, observe that they are symmetric about the \(x\)-axis, ie, they have vertical symmetry. Stated formally, if \((x, y)\) is a point satisfying \(y^2 = x^3 + ax + b\), then its reflection \((x, -y)\) across the \(x\)-axis is also a point satisfying the same equation! If \(P = (x, y)\) is a point on a curve defined by a Weierstrass equation, we define \(-P\) to be this reflection \((x, -y)\). (Careful: we only invert the \(y\)-coordinate of \(P\) to get \(-P\), not both coordinates!)

Here is the second property: if I pick any two points on the curve, the unique line that passes through those two points will have a unique “other” point of intersection with the curve. Well, almost…! But we will get to this almost soon. First, here is an example:

Consider the Weierstrass equation \[ y^2 = x^3 + 17. \] It is nonsingular because \[ \Delta = -16(4 \cdot 0^3 + 27 \cdot 17^2) = -16 \cdot 27 \cdot 17^2 \neq 0. \] Consider the points \(P = (-2, 3)\) and \(Q = (-1, 4)\). Both of these lie on the curve, as you should verify:

There is a unique “secant” line that passes through these two points. We can calculate its slope using the usual rise-over-run formula as \[ m = \frac{4 - 3}{-1 - (-2)} = \frac{1}{1} = 1 \] and then we can find the equation of the secant line itself using point-slope form: \[ \begin{aligned} y - 4 &= 1 \cdot (x - (-1)) \\ y &= x + 5 \end{aligned} \] Let’s now think about intersecting this secant line with the curve. This will consist of all \((x, y)\) which satisfy both \(y = x + 5\) and also \(y^2 = x^3 + 17\), so if we substitute the first equation in the second, we see that we must have \[ \begin{aligned} (x+5)^2 &= x^3 + 17 \\ x^2 + 10x + 25 &= x^3 + 17 \\ x^3 - x^2 - 10x - 8 &= 0 \end{aligned} \] We now have to solve a cubic equation, which isn’t easy in general, but here’s the trick: we already know that \(x = -2\) and \(x = -1\) must be solutions to this equation! After all, we know that \(P = (-2, 3)\) and \(Q = (-1, 4)\) are on the curve and on the line, and the \(x\)-coodinates of these points are precisely \(-2\) and \(-1\). This means that \((x+2)(x+1) = x^2 + 3x + 2\) must divide \(x^3 - x^2 - 10x - 8\), and we can use polynomial long division to find the quotient.

The upshot is that \(x^3 - x^2 - 10x - 8 = (x+2)(x+1)(x-4)\), so the third solution to the cubic equation \(x^3 - x^2 - 10x - 8 = 0\) is \(x = 4\). If we plug \(x = 4\) into the equation of the line, we find the point \(R = (4, 9)\). We already know by construction that this point \(R\) must satisfy the Weierstrass equation too, but you should check this:

Here is the picture of what we’ve just done:

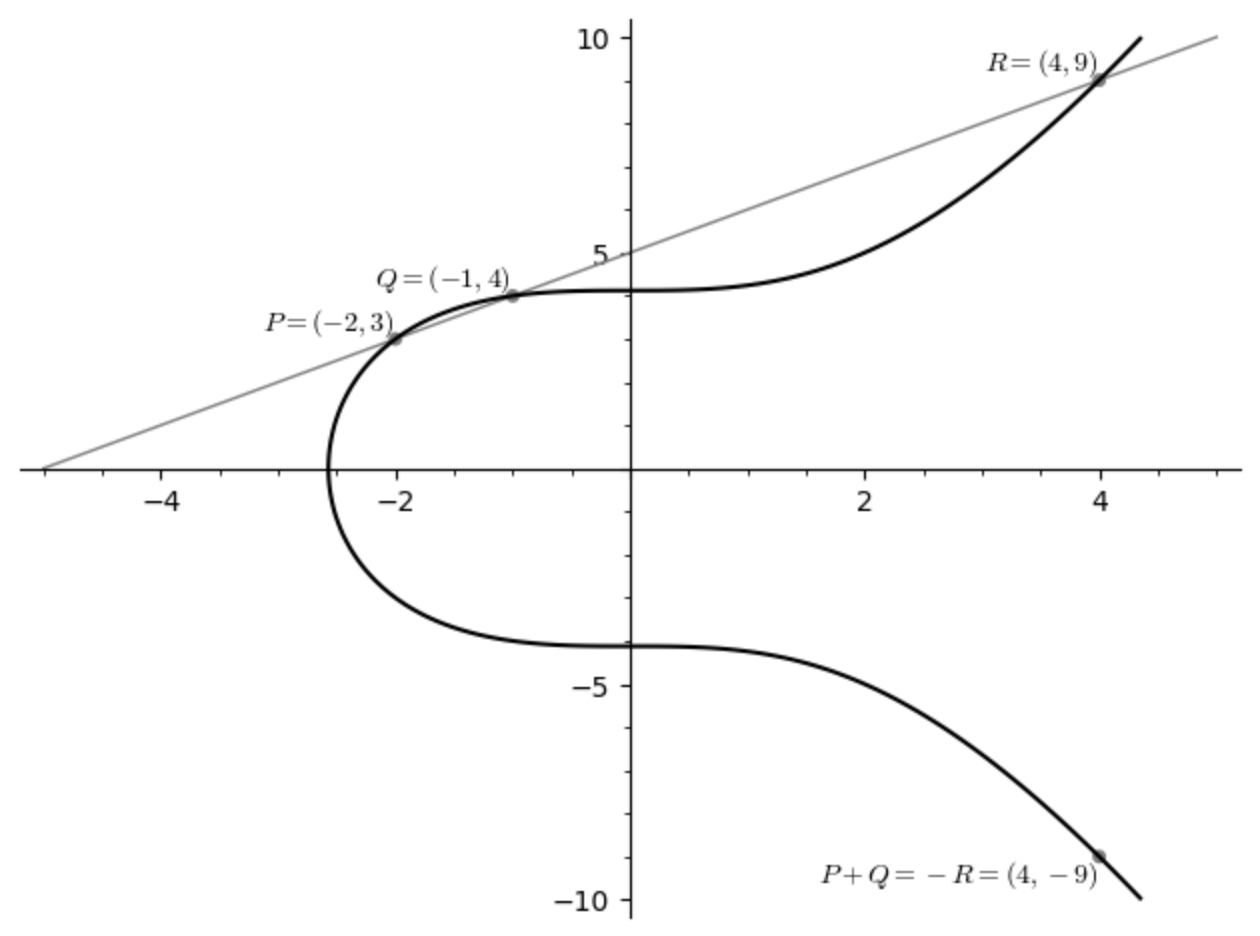
As indicated in the picture, we will define \(P+Q\) to be the negative of this third point of intersection. Be careful: this process is much more complicated than simply adding the \(x\) and \(y\) coordinates of the two points! You should do the following exercise before proceeding:

Let’s now return to the “almost” we mentioned above. In fact, this “almost” actually encompassed two caveats that we need to discuss.

The first caveat has to do with the case when the two points we start with are the same point. Consider again the situation \(P = (-2, 3)\). How can we make sense of \(P + P\), or \(2P\)? The very first step involves finding the equation of the secant line that passes through \(P\) and \(P\), but there isn’t a unique such line…!

But, if you think back to your calculus classes, you might remember that: if you think about the secant lines through two points on a curve, and take the limit as one of the two points approaches the other, what you wind up with is the tangent line! So we’ll use this. In other words, to define \(P + P\), we’ll go through the same process that we did above, but we’ll use the tangent line of the curve at \(P\).

Let’s work this out. To find the slope of the tangent line, we use implicit differentiation on the equation \(y^2 = x^3 + 17\). We get \[ 2y \frac{dy}{dx} = 3x^2 \] and then we plug in \(P = (x, y) = (-2, 3)\) to get \[ \begin{aligned} 2 \cdot 3 \cdot \left.\frac{dy}{dx}\right|_P &= 3(-2)^2 \\ \left.\frac{dy}{dx}\right|_P &= 2 \end{aligned} \] We then find the equation of the tangent line again using point-slope form like we did above: \[ \begin{aligned} y - 3 &= 2(x - (-2)) \\ y &= 2x + 7 \end{aligned} \] We now want to intersect this point with the curve, so we again substitute \(y = 2x+7\) into \(y^2 = x^3 + 17\) like we did above: \[ \begin{aligned} (2x+7)^2 &= x^3 + 17 \\ 4x^2 + 28x + 49 &= x^3 + 17 \\ x^3 - 4x^2 - 28x - 32 &= 0 \end{aligned} \] We again have a cubic equation to factor. Last time, we knew two factors of the cubic because we knew two points on the intersection. This time, we only know one point of the intersection, but we know that the line is tangent to the curve at \(P\), so the \(x\)-coordinate of \(P\), ie \(x = -2\), must be a double root of this cubic! This means that the cubic must be divisible by \((x-(-2))^2 = x^2 + 4x + 4\), and we can again use polynomial long division to find the “third” point of intersection.

This means that the third point of intersection has \(x\)-coordinate 8, so its \(y\)-coordinate is \(2 \cdot 8 + 7 = 23\). We then reflect this point across the \(x\)-axis and find that \(2P = (8, -23)\). Here is a picture of what we have just done:

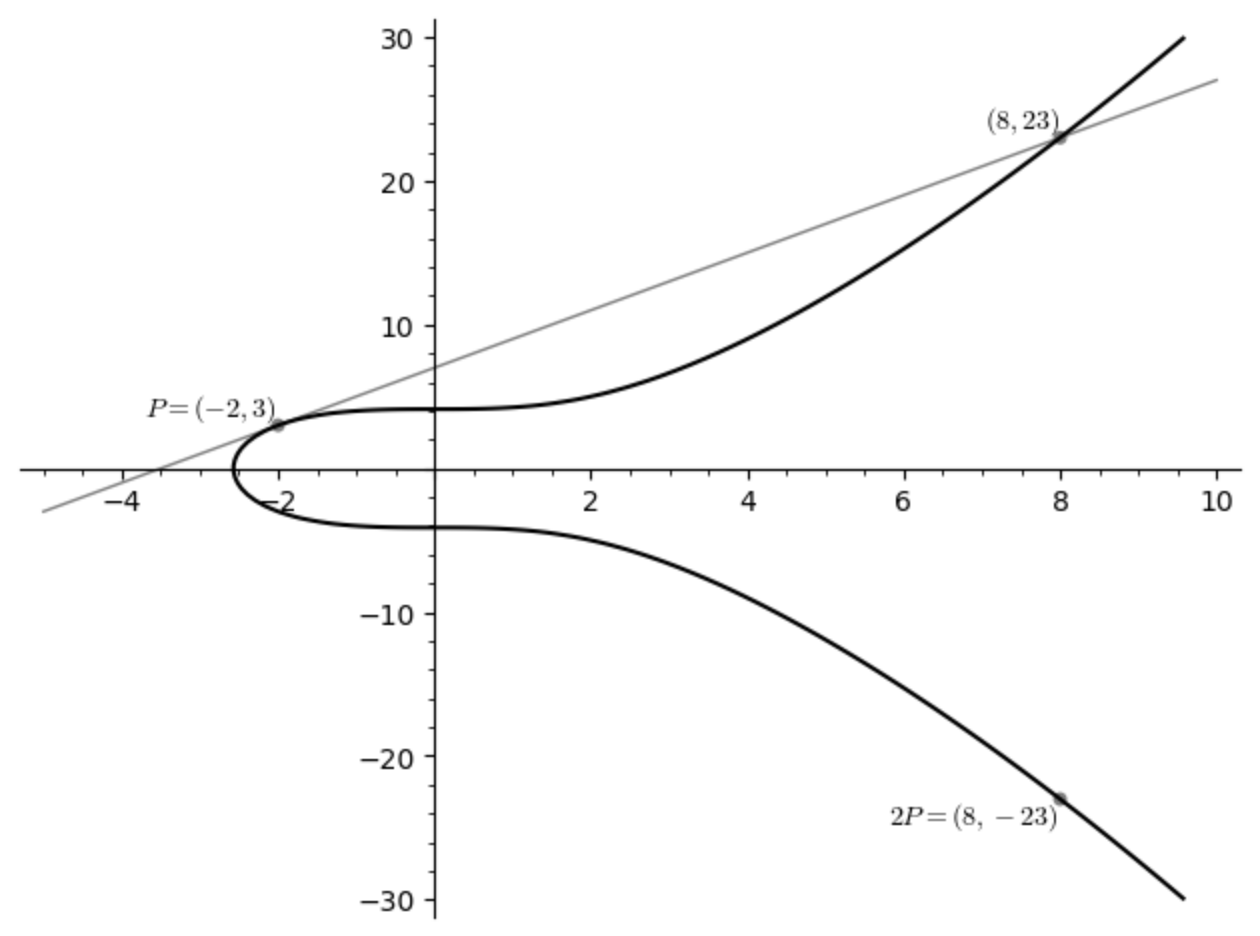
Note that the curve looks different from the previous picture only because of the scale on the axes; it is the same curve.

This brings us to the second caveat that was encompassed by our “almost.” There is one situation when the line passing through two points (either the secant line through two distinct points or the tangent line at a single point) does not have a third point of intersection with the curve. This will happen precisely when the line ends up being vertical! This should be clear from the geometry, but you should verify it algebraically:

We deal with this by fiat. We declare that there is a point, denoted \(O\) and called the point at infinity, which is a point on the curve defined by \(y^2 = x^3 + 17\) and is also a point on every vertical line in the plane. It is its own negative. Thus, if we’re trying to “add” two points and encounter the situation where a secant or tangent line is vertical, we declare the sum to be \(O\).

Having worked through this extended example, we can now make some formal statements.

If you’ve taken some abstract algebra, you’ll probably recognize that the above is saying that \(E\) is an “abelian group” — but don’t worry about this if you don’t know what this means.

It is also useful to generalize the calculations we did above and derive the following general formulas:

Let’s conclude our discussion of elliptic curves over the reals with one more concrete example. This is another highly recommended exercise!

We can compute multiples of a point by using the same idea as binary exponentiaton — except that maybe it’s better to call it “binary multiplication” in this situation. Consider \(P = (-2, 3)\) on the elliptic curve defined by \(y^2 = x^3 + 17\) again. Let’s say that we want to compute \(6P\), ie, the sum of \(P\) with itself 6 times. The idea is to double repeatedly: \[ \begin{aligned} P &= (-2, 3) \\ 2P &= (8, -23) \\ 4P &= 2(2P) = \left(\frac{752}{529}, -\frac{54239}{12167}\right) \end{aligned} \] We then put these together: \[ 6P = 4P + 2P = \left(\frac{752}{529}, -\frac{54239}{12167}\right) + (8, -23) = \left( -\frac{4471631}{3027600}, -\frac{19554357097}{5268024000} \right). \]

We also make the following definition of order.

4.10. Interlude: Elliptic Curves Mod a Prime

We now fix a prime \(p\). For technical reasons that not worth lingering on for our cryptographic purposes, we should assume \(p \neq 2, 3\), ie, that \(p \geq 5\). (In applications to cryptography, \(p\) will anyway be very very large!)

We start with adapting our definitions above as follows.

Consider, for example, the Weierstrass equation \(y^2 = x^3 + 17\). It is integral since \(a = 0\) and \(b = 17\) are integers. We calculated earlier that \[ \Delta = -16 \cdot 27 \cdot 17^2. \] The only primes this is divisible by are 2, 3, and 17. Thus the equation \(y^2 = x^3 + 17\) is singular mod \(p = 17\), but nonsingular otherwise (recall that we are anyway ruling out \(p = 2, 3\)).

When we have an integral Weierstrass equation \(y^2 = x^3 + ax + b\), we can consider its “solutions mod \(p\).” By this we mean integers \((x, y)\) such that \(y^2 \equiv x^3 + ax + b \pmod{p}\). For example, suppose \(p = 7\) and consider the Weierstrass equation \(y^2 = x^3 + 17\). Then \((1, 2)\) is a solution to the equation mod \(p\) because \[ y^2 = 2^2 = 4 \equiv 18 = 1^3 + 17 = x^3 + 17 \pmod{7}. \] Let’s define that, if \(x, y, x', y'\) are all integers, then \((x, y) \equiv (x', y') \pmod{p}\) means that \(x \equiv x' \pmod{p}\) and \(y \equiv y' \pmod{p}\). Notice that, if \((x, y)\) is a solution mod \(p\) of \(y^2 = x^3 + ax + b\), then so is any pair of integers that is congruent mod \(p\). In the example above, observe that \((1, 9)\) or \((8, 2)\) or \((-6, 9)\) are all congruent mod 7 to \((1,2)\), and they are all also solutions mod 7 to \(y^2 = x^3 + 17\). We’ll typically only consider solutions \((x, y)\) where \(0 \leq x, y < p\), in order to avoid having to list off all of the congruent solutions.

It doesn’t really make sense to visualize (congruence classes of) solutions to Weierstrass equations mod \(p\) in the same way that we visualized solutions over the real numbers. Nonetheless, we can take the formulas that we derived using the geometry we discussed above (eg, the Elliptic Curve Addition Formula Theorem), and use the same formulas to make sense of elliptic curves mod \(p\). These formulas look very strange in isolation, but it is important to remember where they come from: they come from the same geometry involving secant and tangent lines that we discussed above! If you understand that geometry, you can do all of the same calculations “mod \(p\)” and derive the formulas that appear below.

Let’s do an example. Consider again \(p = 7\) and the Weierstrass equation \(y^2 = x^3 + 17 \equiv x^3 + 3 \pmod{7}\). We’ve already seen that \(P = (1, 2)\) is a solution to this equation. You should verify for yourself that \(Q = (3, 4)\) is also a solution to this equation. Let’s think about computing \(P + Q\) in “two” ways (but, as you’ll see, they’re both really the same thing).

The first way is just to go through the above formulas carefully. Notice that \(P \neq Q\) and \(x_2 - x_1 = 3 - 1 = 2\) is invertible mod 7 because \(\gcd(2, 7) = 1\). Its inverse is 4 (which we can compute by eyeballing since the numbers are small enough in this case, but in general we would use the extended euclidean algorithm). Thus \[ \begin{aligned} \lambda &= (y_2 - y_1)(x_2 - x_1)^{-1} \bmod{p} \\ &= (4 - 2)(3 - 1)^{-1} \bmod{7} \\ &= 2 \cdot 4 \bmod{7} = 1. \end{aligned} \] Then \[ \begin{aligned} \nu &= y_1 - \lambda x_1 \bmod{p} \\ &= 2 - 1 \cdot 1 \bmod{7} = 1 \\ x_3 &= \lambda^2 - x_1 - x_2 \bmod{p} \\ &= 1^2 - 1 - 3 \bmod{7} = 4 \\ y_3 &= \lambda x_3 + \nu \bmod{p} \\ &= 1 \cdot 4 + 1 \bmod{7} = 5 \end{aligned} \] Thus \(R = (4, 5)\) and \(P + Q = -R = (4, -5 \bmod{7}) = (4, 2)\).

The second way (which, again, is really the same way!) is to remember the geometry that underlies these formulas and use that geometry to guide your calculations; you just have to remember to do your calculations “mod 7” instead. We’re trying to add two distinct points, so the first step is to find the line that passes through those points. We compute the slope of that line as rise-over-run, ie, as \((y_2 - y_1)/(x_2 - x_1)\) — but we have to do this calculation “mod 7,” so instead of dividing, we’ll multiply by a modular inverse. In other words, we really compute \[ (4 - 2)(3 - 1)^{-1} = 2 \cdot 2^{-1} \equiv 2 \cdot 4 = 8 \equiv 1 \pmod{7}. \] Notice that this is the same as the value of \(\lambda\) that we computed above. The next step is to use point-slope form to find the equation of the secant line: we now know it has slope 1, and it passes through \((1, 2)\), so its equation should be \(y - 2 = 1(x - 1)\), or \(y = x + 1\). Notice that this \(y\)-intercept matches what we computed for \(\nu\) above. We next want to intersect this secant line with the curve. We substitute \(y = x + 1\) into \(y^2 = x^3 + 3\) and get \[ \begin{aligned} (x+1)^2 &= x^3 + 3 \\ x^2 + 2x + 1 &= x^3 + 3 \\ x^3 - x^2 - 2x + 2 &= 0 \end{aligned} \] We now need to find the roots of this cubic mod 7. We know that 1 and 3 are roots, so \((x-1)(x-3) = x^2 - 4x + 3\) must divide this cubic.

The fact that the quotient is \(x-4\) tells us that the third point of intersection of the secant line with the curve has \(x\)-coordinate 4, so its \(y\)-coordinate must be \(y = x + 1 = 4 + 1 = 5\). This gives us the same point \(R = (4, 5)\) that we found earlier, and then we “reflect” across the \(x\)-axis to get \[ P + Q = (1, 2) + (3, 4) = (4, -5 \bmod{7}) = (4, 2), \] just as we did before.

Again, we can quickly compute large multiples of a point using the same “binary multiplication” idea.

We can also make the following definition of order.

Unlike in the real case, we don’t need to worry about infinite order anymore:

We also have the analogs of the First and Second Lemmas about Orders in this case:

If you haven’t seen any group theory, you can just take these lemmas for granted. But if you have studied some group theory, I highly encourage you to work through the following exercise:

Here are some concrete examples:

Having developed all of this theory, we can now state the basic problem that underlies elliptic curve cryptography. You should compare it with the discrete logarithm problem that we discussed above:

The naive method for doing this is to just try all the values of \(k\) starting from \(k = 0\) all the way up to \(k = \mathrm{ord}_E(P) - 1\), but if \(\mathrm{ord}_E(P)\) is very large, this will be very slow! There are slightly faster methods than this that work in general. There are also substantially faster methods that work in special cases. But we do not know of anything that is substantially faster in general, which means that by choosing \(p, E, P\) judiciously, we can make the Elliptic Curve Discrete Logarithm Problem intractable for an adversary. This intractability can then be used for cryptographic purposes, in much the same way that the intractibility of the usual Discrete Logarithm Problem can be.

The National Institute of Standards and Technology (NIST) just published (on February 3rd, 2023) a document describing which elliptic curves are currently thought to be safe to use for cryptography; you can browse this document here.

4.11. Elliptic Curve Diffie-Hellman

Let’s start with the elliptic curve variant of the Diffie-Hellman key exchange. Alice and Bob publicly agree to fix a prime \(p\), an elliptic curve \(E\) mod \(p\) (specified by integers \(a, b\) such that the Weierstrass equation \(y^2 = x^3 + ax + b\) is nonsingular mod \(p\)), and a point \(P \in E\). To ensure security, we need for \(\mathrm{ord}_P(E)\) to be large. The data \((p, E, P)\) is all shared publicly.

Alice then chooses a secret integer \(0 \leq k_a < \mathrm{ord}_E(P)\) and sends Bob \(Q_a = k_a P\). She can compute this value quickly using binary multiplication. Bob similarly chooses a secret integer \(0 \leq k_b < \mathrm{ord}_E(P)\) and sends Alice \(Q_b = k_b P\). Alice computes \(R = k_a Q_b\), and Bob computes \(R = k_b Q_a \bmod{p}\). The two values of \(R\) that Alice and Bob compute are the same, because \[ k_aQ_b \equiv k_a(k_bP) = k_ak_bP = k_b(k_aP) = k_bQ_a. \] Thus Alice and Bob now share a secret point \(R\) on the elliptic curve.

4.12. Interlude: Quadratic Residues

A familiar feature of the real numbers is that some numbers do not have square roots (namely, the negatives). The same thing happens when you work mod an integer. For example, let \(n = 5\). We know that integer is congruent to 0, 1, 2, 3, or 4 mod 5. This means that any square must be congruent to \(0^2 = 0, 1^2 = 1, 2^2 = 4, 3^2 \equiv 4 \pmod{5}\), or \(4^2 \equiv 1 \pmod{5}\). In other words, only 0, 1, or 4 have square roots mod 5 — and 2 and 3 do not!

We’ll see below that it will be useful to quickly determine whether an integer \(a\) is a quadratic residue mod a prime \(p \geq 3\). It turns out that there is a good way to do this! Let us first introduce the following notation:

For example, we saw above that 4 is a quadratic residue mod 5, so \[ \left( \frac{4}{5} \right) = 1 \] and we saw that 2 is not a quadratic residue mod 5, so \[ \left( \frac{2}{5} \right) = -1. \] We can now rephrase our goal: we would like a quick way of computing Legendre symbols. This is provided to us by combining binary exponentiation with the following:

Proof. There are three cases to consider:

1. \(a \equiv 0 \pmod{p}\);
2. \(a \not\equiv 0 \pmod{p}\) and \(a\) is a quadratic residue mod \(p\); and
3. \(a \not\equiv 0 \pmod{p}\) and \(a\) is not a quadratic residue mod \(p\).

In case (1), the statement we’re trying to prove is clear since both sides of the congruence are 0 mod \(p\). In case (2), there exists an integer \(x\) such that \(x^2 \equiv a \pmod{p}\). Since \(p\) does not divide \(a\), it also does not divide \(x^2\), so it cannot divide \(x\) either by Euclid’s Lemma. Thus \(\gcd(x, p) = 1\), and Euler’s Theorem implies that \[ a^{(p-1)/2} \equiv (x^2)^{(p-1)/2} = x^{p-1} = x^{\phi(p)} \equiv 1 = \left( \frac{a}{p} \right) \pmod{p}. \]

Now consider case (3). The idea is to calculate \((p-1)!\) mod \(p\) in two different ways, by “pairing off” the numbers in two different ways. The first way is to pair them off into pairs \(x, y\) where \(xy \equiv 1 \pmod{p}\). There are 2 “degenerate” pairs where \(x = y\), namely, \(x = y = 1\) and \(x = y = p-1\) (cf. Lemma 4.4.1), but the remaining numbers \(2, \dotsc, p-2\) are all paired off with a different number in the same range and the product of each of those “nondegenerate” pairs is 1, so the Modular Arithmetic Theorem implies that \[ (p-1)! = 1 \cdot 2 \cdot 3 \cdots (p-3) (p-2) (p-1) \equiv 1 \cdot (p-1) \equiv -1 \pmod{p}. \] (This fact is sometimes called Wilson’s Theorem.) On the other hand, we can also pair the numbers off into pairs \(x, y\) where \(xy \equiv a \pmod{p}\). Since we are in case (3) and \(a\) is not a quadratic residue mod \(p\), we know that there is no solution to this congruence where \(x = y\), ie, there are no “degenerate” pairs in this case. There are \((p-1)/2\) pairs, and the product of each pair is \(a\), so the Modular Arithmetic Theorem again guarantees that \[ (p-1)! = 1 \cdot 2 \cdots (p-2) \cdot (p-1) \equiv a^{(p-1)/2} \equiv{p}. \] Thus we have \[ a^{(p-1)/2} \equiv (p-1)! \equiv -1 = \left( \frac{a}{p} \right) \pmod{p} \] and we are done. \(\Box\)

Euler’s Criterion means that we have an efficient algorithm for determining whether something is a quadratic residue: we simply use binary exponentiation to compute \(a^{(p-1)/2} \bmod{p}\) and we can read off the answer! For example, suppose we want to know if \(a = 37\) is a quadratic residue mod \(p = 97\). We have \((p-1)/2 = 96/2 = 48\), so we compute \(a^{(p-1)/2} = 37^{48} \bmod{97}\) using binary exponentiation, and we find that it is \(96 \equiv -1 \pmod{97}\). Euler’s Criterion says that \[ \left( \frac{37}{97} \right) \equiv 37^{(97-1)/2} = 37^{48} \equiv -1 \pmod{97}, \] which means that 37 is not a quadratic residue mod 97.

There is a lot more that can be said about quadratic residues, though this will be roughly enough for our purposes. If you are interested in reading more, you should look up the Tonelli-Shanks algorithm for computing square roots mod \(p\). You might also read more about Jacobi symbols, Kronecker symbols, and quadratic reciprocity.

4.13. Elliptic Curve Elgamal

There is also a variant of the Elgamal cryptosystem using elliptic curves that can be used to exchange messages, but there is a nontrivial encoding step. To make Elgamal work with elliptic curves, we first need a way to encode a plaintext message as a point on an elliptic curve \(E\) mod \(p\).

There is a probabilistic algorithm for doing this. The rough idea is that we can try to encode plaintext as the \(x\)-coordinate of a point, but note that not every integer will occur as the \(x\)-coordinate of a point on an elliptic curve mod \(p\)! Specifically, if \(E\) is given by \(y^2 = x^3 + ax + b\) and if \(P = (x, y)\) is a point on the curve, then the \(x\)-coordinate must have the property that \(x^3 + ax + b\) is a quadratic residue mod \(p\).

Entire Process

Let us start by describing the Elgamal process in its entirety and in the abstract.

Suppose that Bob would like to be able to receive messages of length \(N\). Bob will fix a positive integer \(s\). We will see that, the larger that Bob chooses this integer, the higher the probability that encoding will succeed. Bob will then choose a prime \(p > s26^N\), and an elliptic curve \(E\) mod \(p\) (defined by integers \(a, b\) such that the integral Weierstrass equation \(y^2 = x^3 + ax + b\) is nonsingular mod \(p\)), and a point \(P \in E\). He computes \(\mathrm{ord}_E(P)\). Then Bob chooses a secret integer \(0 \leq k < \mathrm{ord}_E(P)\) to serve as his private key. He computes \(Q = kP\), and this value is part of his public key. In other words, Bob will share all of the data \((s, E, P, \mathrm{ord}_E(P), Q)\) publicly, and keep only the integer \(k\) secret.

Suppose now that Alice wants to send Bob a message. She first converts her message into an integer \(m\) using the same base 26 idea we used for RSA. She will then iterate through values of \(r = 0, 1, 2, \cdots, s-1\) until she finds the first value of \(x = sm + r\) such that \[ \left( \frac{x^3 + ax + b}{p} \right) \neq -1. \] Note that that the maximum possible value of \(m\) is \(26^N - 1\), so \[ x = sm + r < s(26^N-1) + s = s26^N < p, \] since Bob chose \(p\) to be larger than \(s26^N\). There is a roughly 1/2 chance that an integer in \([0, p)\) is not a quadratic residue mod \(p\), and here we are iterating through \(s\) integers in the range \([0, p)\), so there is a \(1/2^s\) chance that \(x^3 + ax + b\) is not a quadratic residue for any of the \(s\) possible values of \(x = sm + r\). If none of the \(s\) integers are quadratic residues, encoding fails — but if Bob chose \(s\) to be even moderately large, encoding failure is very unlikely! If encoding does fail, Alice can just modify her message slightly (rephrase slightly? add a nonsense letter?) and try encoding again. Once Alice is able to find a value of \(x\) such that \(x^3 + ax + b\) is a quadratic residue mod \(p\), then there is a integer \(y\) such that \(y^2 \equiv x^3 + ax + b \pmod{p}\), so the point \(M = (x, y)\) is on \(E\). This will be the encoding of her plaintext message.

This is not yet the ciphertext, but at this point she can encrypt the encoded message using a process very similar to the Elgamal cryptosystem we discussed earlier. Alice chooses an “ephemeral key” \(h\) such that \(0 \leq h < \mathrm{ord}_E(P)\). She computes \(S = hQ\), \(R_1 = hP\), and \(R_2 = M + S\). The pair \((R_1, R_2)\) is the ciphertext that she sends to Bob.

To decrypt the ciphertext \((R_1, R_2)\), Bob uses his private key \(k\) to compute \(S = kR_1\). Observe that \[ kR_1 = k(hP) = khP = h(kP) = hQ, \] so Bob has found the same value of \(S\) that Alice had, even though he does not know the value of the ephemeral key \(h\). He can then compute \(-S\) by negating the \(y\)-coordinate, and he then calculates \[ R_2 - S = R_2 + (-S) = (M + S) + (-S) = M + (S + (-S)) = M + O = M. \] He has thus recovered Alice’s encoded plaintext!

Finally, Bob just needs to decode \(M\). If \(M = (x, y)\), he can extract the first coordinate \(x\). The quotient when he divides this by \(s\) is the integer \(m\) that represents the message in base 26, so he then finishes off by converting back to text using the same process we used for RSA above.

Whew!

Encoding and Decoding

Here are some exercises to help you understand the above process by breaking it down and working with some pieces. First up are the encoding and decoding parts of the process (careful: not the encryption and decryption yet).

Encryption and Decryption

Here is an example of the encryption and decryption process in a small example and using Sage. I encourage you to follow along and type things into a SageCell yourself as you read through this example (or you can do the calculations by hand, though this might get a little tiring even in this small example).

When generating his elliptic curve Elgamal public key, Bob chooses the elliptic curve \(E\) defined by \(y^2 = x^3 + 3x + 4\) mod \(p = 7\) and the point \(P = (5, 5) \in E\).

E = EllipticCurve(GF(7), [3, 4])
P = E(5, 5)

By running P.order(), we find that \(\mathrm{ord}_E(P) = 10\). Suppose Bob chooses the secret integer \(k = 3\). By typing 3*P into Sage, he finds that \(Q = kP = 3 \cdot (5, 5) = (2, 5)\). All parts of this calculation except the value of \(k = 3\) are made public; \(k\) is his private decryption key.

Now suppose Alice wants to send Bob a message. She sets up her Sage session by pulling the following information from Bob’s public key.

E = EllipticCurve(GF(7), [3, 4])
P = E(5, 5)
order = 10
Q = E(2, 5)

Suppose that, following the encryption process described above, her encoded message is the point \(M = (0, 5)\). She chooses an ephemeral key between \(0\) and \(\mathrm{ord}_E(P) = 10\), say \(h = 4\). She must keep this value of \(h\) secret. She computes \(R_1 = hP\) by typing \(4 * P\) into Sage and finds \(R_1 = (0, 2)\). She then computes \(R_2 = M + S = M + hQ\) by typing E(0, 5) + 4*Q into Sage and finds \(R_2 = (1, 6)\). The pair \((R_1, R_2) = ((0, 2), (1, 6))\) is the ciphertext that she sends to Bob.

Let’s now go backwards and check that Bob is able to recover Alice’s message. He computes \(M = R_2 - kR_1\) by typing E(1, 6) - 3*E(0, 2) and finds \(M = (0, 5)\), which was Alice’s encoded message!